Mahmoud Abdelkhalek

Problem statement

We show how to solve this problem using an example input. We first describe a solution that requires $O(N)$ time and space, where $N$ is the length of the height array. Then, we explain how to further optimize this solution to reduce the space required to $O(1)$.

Preliminaries

Consider the input array height = [0,2,0,3,1,0,1,3,2,1]. The maximum area of water trapped for this height array is shown in Fig. 1.

Maximum area of rain water trapped for height = [0,2,0,3,1,0,1,3,2,1]. — **Fig. 1**: Maximum area of rain water trapped for `height = [0,2,0,3,1,0,1,3,2,1]`.

We then overlay the amount of water trapped at the $i$th position, as shown in Fig. 2.

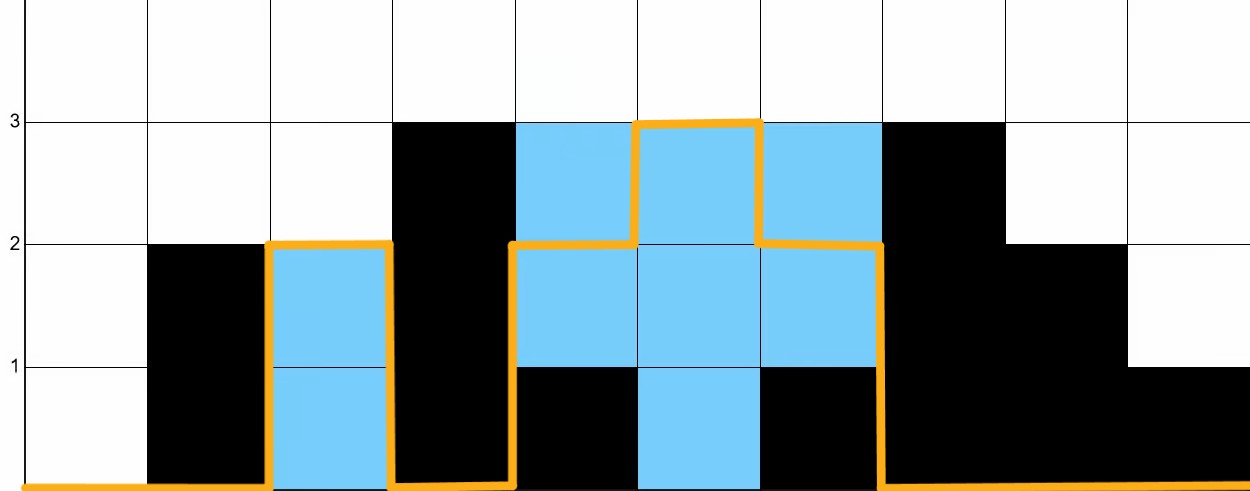
**Fig. 2**: The amount of water trapped at the $i$th position based on Fig. 1.

The amount of water that can be trapped at the $i$th position is shown in orange. The orange line also corresponds to a plot of the function $f : {0,1,\dots,N-1} \to \mathbb N \cup {0}$, where $N$ is the length of the height array, that returns the amount of water that can be trapped at the $i$th position in the height array.

The total amount of water trapped is equivalent to the area under the orange line. That is, we compute the total area of water trapped as $A = \sum_{k=0}^{N-1} f(k)$.

Decomposing $f$

The function $f$ can be decomposed as the difference between the “envelope” of the bars in Fig. 2 and the height of the bars, as shown in Fig. 3.

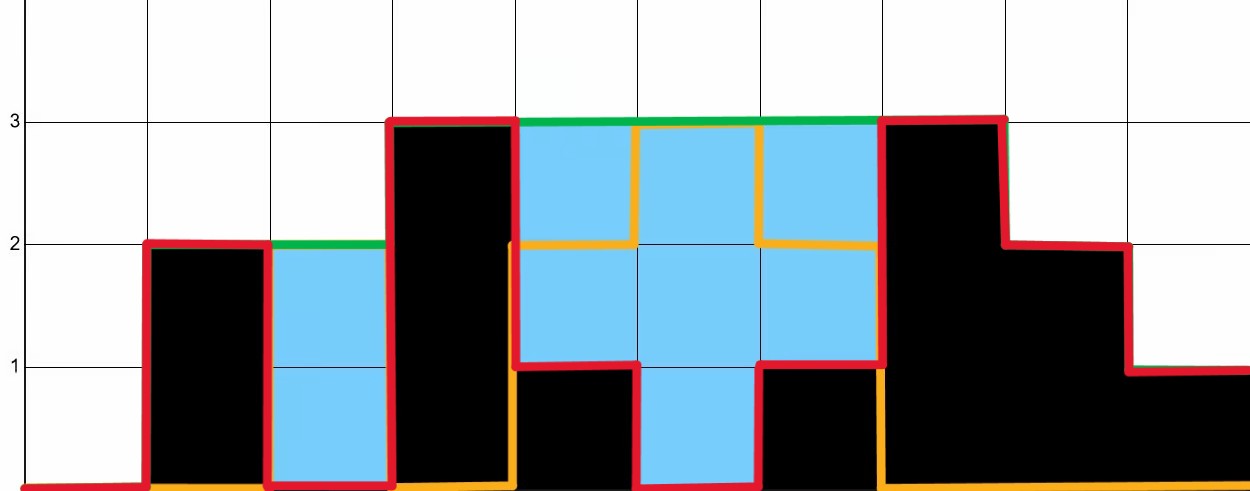
**Fig. 3**: The difference between the envelope of the bars and the height of the bars. The envelope of the bars is shown in green while the height of the bars is shown in red.

In Fig. 3, the function $f$ shown in orange is obtained by subtracting the red line (bar heights) from the green line (envelope). Our goal then is to construct the green and red lines and then subtract them to obtain the function $f$.

We already know how to construct the red line, since it is equivalent to the values in the height array. To construct the green line, we decompose it as the element-wise minimum of two lines, as shown in Fig. 4.

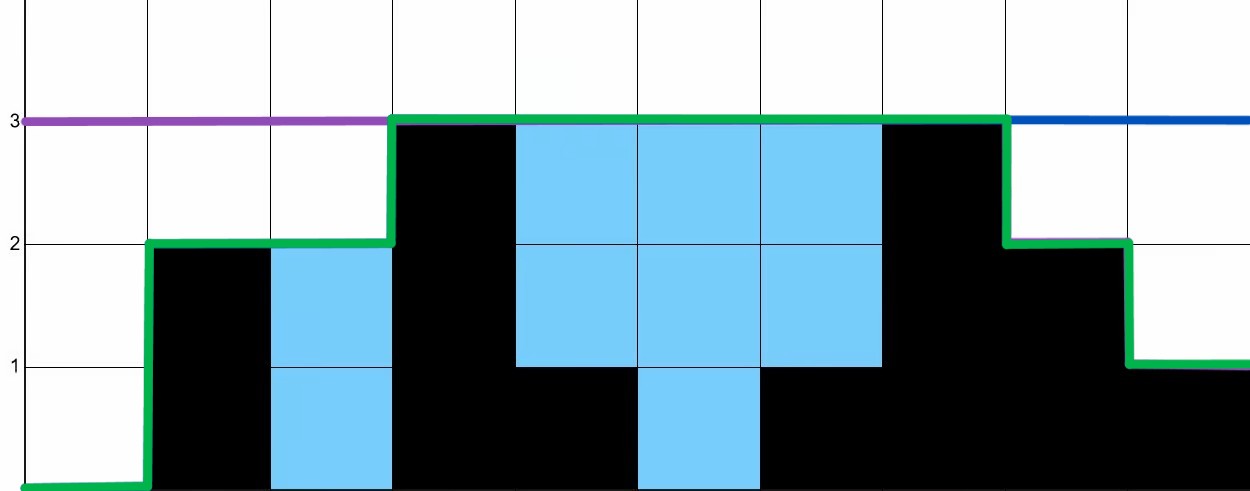
**Fig. 4**: How to construct the envelope of the bars. The envelope is shown in green.

In Fig. 4, the envelope can be decomposed as the minimum of a “left envelope” shown in blue in Fig. 5a and a “right envelope” shown in purple in Fig. 5b.

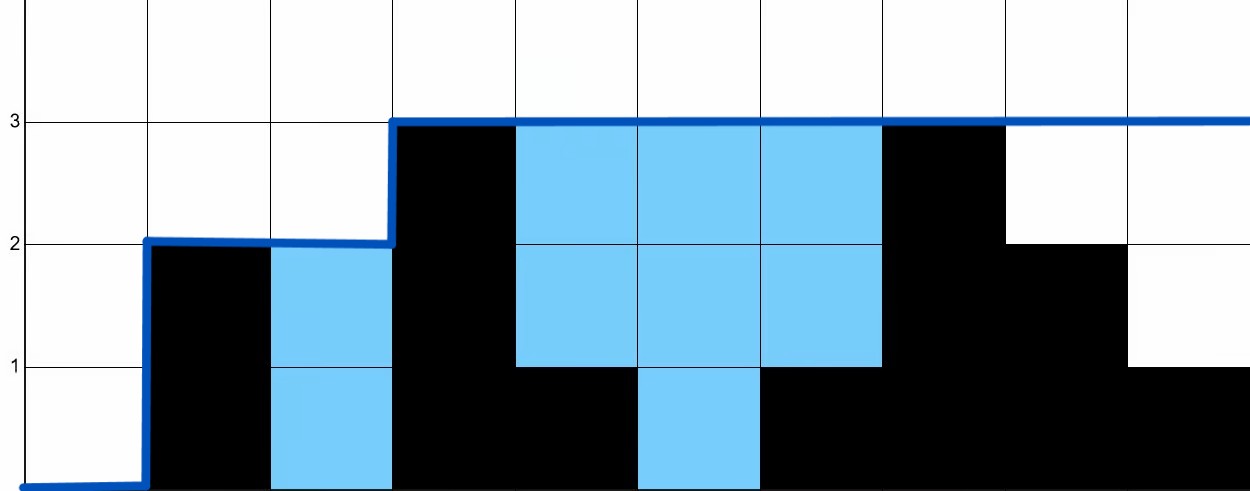
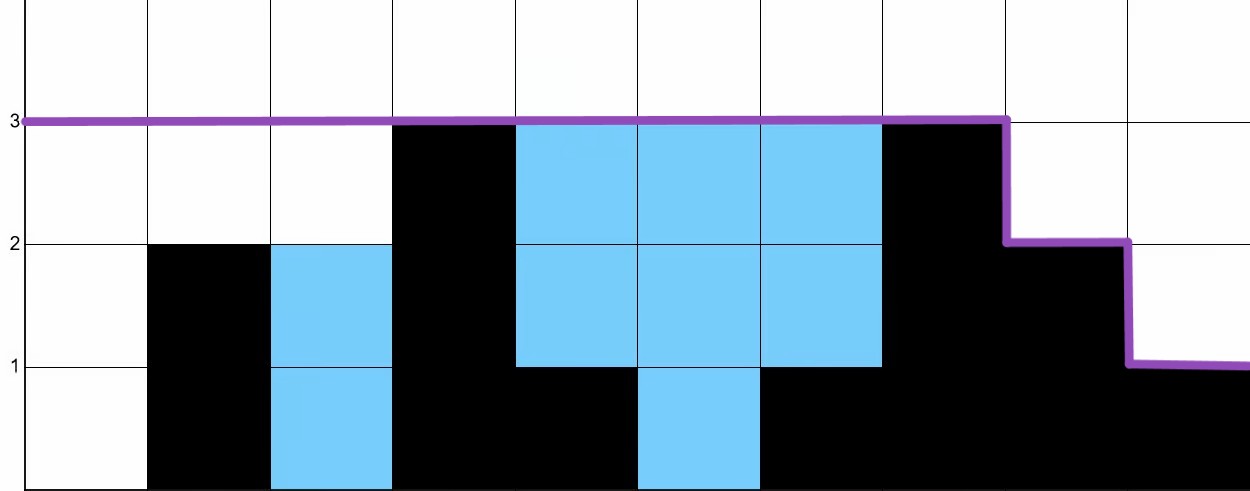
The envelope in Fig. 4 is the result of computing the element-wise minimum of the left and right envelopes shown in Fig. 5a and 5b, respectively.

To summarize, we compute the total area of trapped water as follows:

Decompose $f$ as the difference between the green and red lines shown in Fig. 3.
Decompose the green line into the blue and purple lines shown in Fig. 5a and 5b, respectively.
Compute the heights of the blue and purple lines.
Compute $f$ at each position.
Sum all the outputs of $f$ to obtain the total area of trapped water.

We now describe how to compute the blue and purple lines (i.e. the left and right envelopes).

Computing the left and right envelopes

For convenience, let $\texttt{height}[i] = h_i$.

The left and right envelopes correspond to the cumulative maximum of the bar heights starting from the left and right, respectively. That is, the height of the blue and purple lines in Fig. 5a and Fig. 5b, respectively, at the $i$th position are $\ell_i = \max(h_0, h_1, \dots, h_i)$ and $r_i = \max(h_{N-(i+1)}, \dots, h_{N-2}, h_{N-1})$, respectively.

Because

$$ \begin{align*} \ell_i &= \max(h_0, h_1, \dots h_i) \\ &= \max(\max(\max(\max(h_0, h_1),h_2),h_3), ..., h_i) \\ &= \max(\max(\max(\max(\max(h_0, h_0), h_1),h_2),h_3), ..., h_i) \\ r_i &= \max(h_{N-(i+1)}, \dots, h_{N-2}, h_{N-1}) \\ &= \max(h_{N-(i+1)}, \dots, \max(h_{N-4},\max(h_{N-3}, \max(h_{N-2}, h_{N-1})))) \\ &= \max(h_{N-(i+1)}, \dots, \max(h_{N-4},\max(h_{N-3}, \max(h_{N-2}, \max(h_{N-1}, h_{N-1}))))) \end{align*} $$

we can compute $\ell_i$ recursively forward and $r_i$ recursively backward as

$$ \begin{align*} \ell_i &= \begin{cases} h_0, &i = 0 \\ \max(\ell_{i-1},h_i), &i = 1,\dots,N-1\end{cases} \\ r_i &= \begin{cases} h_{N-1}, &i = N-1 \\ \max(r_{i+1},h_{i}), &i = N-2,\dots,0\end{cases} \end{align*} $$

Computing the envelope, $f$, and the area of water trapped

Once we have computed the left and right envelopes $\ell_i$ and $r_i$ for $i = 0,\dots,N-1$, the envelope shown in Fig. 4 is $e_i = \min(\ell_i,r_i)$ for $i = 0,\dots,N-1$.

The function $f$ is then be computed as $f(k) = e_k - h_k$ for $k = 0,\dots,N-1$ and the total area of water trapped is equal to $A = \sum_{k=0}^{N-1} f(k)$.

Naive solution

We can compute the total area of water $A$ trapped as follows:

Compute the left and right envelopes $\ell_i$ and $r_i$ as two arrays of length $N$.
Compute the envelope $e_i$ as another array of length $N$.
Compute $A$ as $A = \sum_{k=0}^{N-1} f(k) = \sum_{k=0}^{N-1} e_k - h_k$.

This solution can be implemented in Python as follows:

class Solution:
    def trap(self, height: List[int]) -> int:
        l = [height[0]] * len(height)
        for i in range(1,len(height)):
            l[i] = max(l[i-1], height[i])
        r = [height[-1]] * len(height)
        for i in range(len(height)-2,-1,-1):
            r[i] = max(r[i+1], height[i])
        max_area = 0
        for i in range(len(height)):
            max_area += min(l[i], r[i]) - height[i]
        return max_area

This solution requires $O(N)$ time and space. Can we do better?

Optimized solution

We can simplify the naive solution described above to only require $O(1)$ space. The key insight needed to do this is to notice that the sequences $\ell_i$ and $r_i$, for $i = 0,\dots,N-1$, are monotonically increasing and monotonically decreasing, respectively. That is, for $i = 0, \dots,N-1$, $\ell_0 \leq \ell_1 \leq \cdots \leq \ell_i$ and $r_{N-1} \leq r_{N-2} \leq \cdots \leq r_{N-(i+1)}$.

Hence, for every $(i, j) \in \{0,\dots,N-1\}^2$, if $\ell_i \leq r_j$, then $\ell_i \leq r_j \leq r_{j-1} \leq r_{j-2} \leq \cdots \leq r_0$. That is, $\ell_i \leq r_j \implies \min(\ell_i, r_k) = \ell_i$ for every $k = 0, \dots, j$. This means that if $i < j$ and $\ell_i \leq r_j$, then $e_i = \min(\ell_i, r_i) = \ell_i$.

Alternatively, if $r_j < \ell_i$, then $r_j < \ell_i \leq \ell_{i+1} \leq \ell_{i+2} \leq \cdots \leq \ell_{N-1}$. That is, $r_j < \ell_i \implies \min(r_j, \ell_k) = r_j$ for every $k = i, \dots, N-1$. This means that if $i < j$ and $r_j < \ell_i$, then $e_j = \min(r_j, \ell_j) = r_j$.

These “dominance” properties are similar to the ones derived in 11. Container With Most Water and suggest a left and right pointers approach:

Let $i \gets 0$ and $j \gets N-1$ be the left and right pointers, respectively.
Let $A \gets 0$ be a variable that will accumulate the area of water trapped.
Because $i < j$, compute $\ell_i \gets h_0$ and $r_j \gets h_{N-1}$.
While $i < j$,
1. If $\ell_i \leq r_j$,
  1. $e_i \gets \ell_i = \min(\ell_i, r_i)$.
  2. $f_i \gets e_i - h_i$.
  3. $A \gets A + f_i$.
  4. $\ell_{i+1} \gets \max(\ell_i, h_{i+1})$.
  5. $i \gets i + 1$.
2. Else,
  1. $e_j \gets r_j = \min(r_j, \ell_j)$.
  2. $f_j \gets e_j - h_j$.
  3. $A \gets A + f_j$.
  4. $r_{j-1} \gets \max(r_j, h_{j-1})$.
  5. $j \gets j - 1$.
Return $A$.

This optimized solution requires only $O(1)$ space and can be implemented in Python as follows:

class Solution:
    def trap(self, height: List[int]) -> int:
        i, j = 0, len(height) - 1
        A = 0
        l, r = height[i], height[j]
        while i < j:
            if l <= r:
                # e_i \gets \ell_i = \min(\ell_i, r_i)
                e = l
                # f_i \gets e_i - h_i
                f = e - height[i]
                # A \gets A + f_i
                A += f
                # \ell_{i+1} \gets \max(\ell_i, h_{i+1})
                l = max(l, height[i+1])
                # i \gets i + 1
                i += 1
            else:
                # e_j \gets r_j = \min(r_j, \ell_j)
                e = r
                # f_j \gets e_j - h_j
                f = e - height[j]
                # A \gets A + f_j
                A += f
                # r_{j-1} \gets \max(r_j, h_{j-1})
                r = max(r, height[j - 1])
                # j \gets j - 1
                j -= 1
        return A

42. Trapping Rain Water